Odległość edycyjna, najdłuższy wspólny podciąg¶

dr inż. Aleksander Smywiński-Pohl¶

konsultacje: środa 15.00-16.00¶

Niedokładne dopasowywanie łańcucha znaków¶

źródło: https://google.com

źródło: https://en.wikipedia.org/wiki/Sequence_alignment

Odległość edycyjna¶

Dozwolone operacje edycji:

  • dodanie znaku: ac vs. abc
  • usunięcie znaku: abc vs. ac
  • zamiana znaku: abc vs. adc

Odległość edycyjna - minimalna liczba operacji edycji pozwalająca zamienić łańcuch x w y:

  • $edit(x,y) \geq 0$
  • $edit(x,y) = 0 \Leftrightarrow x = y$
  • $edit(x,y) = edit(y,x)$
  • $edit(x,y) \leq edit(x,z) + edit(z,y)$

Obliczanie odległości edycyjnej¶

$$ EDIT[i, j] = edit(x[1..i], y[1..j]) $$
$$ EDIT[0, j] = j $$
$$ EDIT[i, 0] = i $$
$$ \begin{array}{r r l} EDIT[i, j]& = min& \{\\ && EDIT[i-1, j] + 1,\\ && EDIT[i, j-1] + 1,\\ && EDIT[i-1, j-1] + \delta(x[i], y[j])\\ &\}&\\ \end{array} $$

gdzie: $\delta(a, b)$ - koszt operacji zmiany znaku: 0, gdy oba znaki są identyczne, 1 w przeciwnym razie.

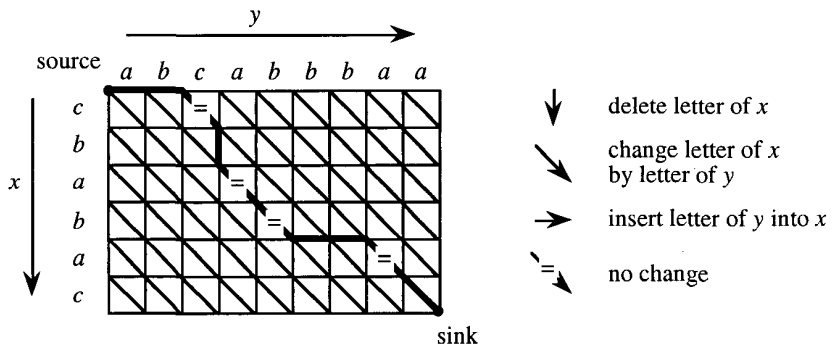
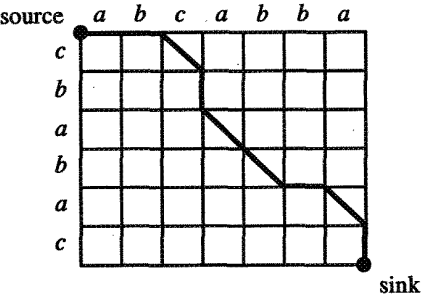
Grafowa reprezentacja problemu¶

$G$ - graf uzgodnień:

  1. $(i,j)$ - węzły grafu, gdzie $0 \leq i \leq |x|$, $0 \leq j \leq |y|$
  1. $(i-1, j-1)$ posiada krawędzie do węzłów:
    • $(i, j-1)$ o koszcie 1,
    • $(i-1, j)$ o koszcie 1,
    • $(i, j)$ o koszcie $\delta(x[i], y[j])$,
    • o ile $i$ oraz $j$ spełniają warunek 1.
  1. odległość edycyjna = waga najmniej kosztownej ścieżki od $(0,0)$ do $(|x|, |y|)$.
In [13]:
import numpy as np

def delta(a, b):
    if a == b:
        return 0
    else:
        return 1

def edit_distance(x, y, delta):
    edit_table = np.empty((len(x)+1, len(y)+1))
    for i in range(len(x)+1):
        edit_table[i, 0] = i
    for j in range(len(y)+1):
        edit_table[0, j] = j
        
    for i in range(len(x)):
        k = i + 1
        for j in range(len(y)):
            l = j + 1
            edit_table[k,l] = min(edit_table[k-1,l]+1, 
                                  edit_table[k,l-1]+1, 
                                  edit_table[k-1, l-1] + delta(x[i], y[j]))
    print(edit_table)
    return edit_table[len(x), len(y)]
In [15]:
edit_distance('wojtk', 'wjeek', delta)

[[0. 1. 2. 3. 4. 5.]
 [1. 0. 1. 2. 3. 4.]
 [2. 1. 1. 2. 3. 4.]
 [3. 2. 1. 2. 3. 4.]
 [4. 3. 2. 2. 3. 4.]
 [5. 4. 3. 3. 3. 3.]]
Out[15]:
3.0
In [7]:
! pip install unidecode

Collecting unidecode
  Downloading Unidecode-1.2.0-py2.py3-none-any.whl (241 kB)
     |████████████████████████████████| 241 kB 2.2 MB/s eta 0:00:01
Installing collected packages: unidecode
Successfully installed unidecode-1.2.0
In [17]:
from unidecode import unidecode

def delta2(a, b):
    if a == b:
        return 0
    elif unidecode(a) == unidecode(b):
        return 0.5
    else:
        return 1
In [16]:
unidecode('Łódź')
Out[16]:
'Lodz'
In [18]:
edit_distance('Łódź', 'Lodz', delta2)
edit_distance('Łódź', 'Żółć', delta2)

[[0.  1.  2.  3.  4. ]
 [1.  0.5 1.5 2.5 3.5]
 [2.  1.5 1.  2.  3. ]
 [3.  2.5 2.  1.  2. ]
 [4.  3.5 3.  2.  1.5]]
[[0. 1. 2. 3. 4.]
 [1. 1. 2. 3. 4.]
 [2. 2. 1. 2. 3.]
 [3. 3. 2. 2. 3.]
 [4. 4. 3. 3. 3.]]
Out[18]:
3.0

Złożoność algorytmu¶

Złożoność czasowa $O(|x| * |y|)$

Złożoność pamięciowa $O(min\{|x|,|y|\})$ -- wariant, w którym pamiętamy tylko bieżący i poprzedni wiersz/kolumnę.

Najdłuższy wspólny podciąg¶

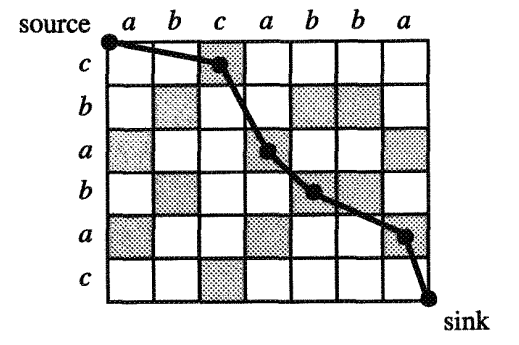
Oznaczenia¶

$lcs(x,y)$ - długość najdłuższego wspólnego podciągu

$LCS[i,j]$ - długość najdłuższego wspólnego podciągu dla $x[1..i]$, $y[1..j]$

$edit_{di}(x,y)$ - odległość edycyjna dla operacji dodania i usunięcia liter (brak zamiany)

$$ EDIT_{di}[i,j] = edit_{di}(x[1..i], y[1..j]) $$

Lemat (4.1)¶

$2 * lcs(x,y) = |x| + |y| - edit_{di}(x,y)$

$2 * LCS[i,j] = i + j - EDIT_{di}[i,j]$

dla $0 \leq i \leq |x|$, $0 \leq j \leq |y|$

In [111]:
def delta2(x,y):
    if x == y:
        return 0
    else:
        return 2

def lcs1(x, y):
    return (len(x) + len(y) - edit_distance(x,y,delta2))/2

lcs1('cbabac', 'abcabba')

[[0. 1. 2. 3. 4. 5. 6. 7.]
 [1. 2. 3. 2. 3. 4. 5. 6.]
 [2. 3. 2. 3. 4. 3. 4. 5.]
 [3. 2. 3. 4. 3. 4. 5. 4.]
 [4. 3. 2. 3. 4. 3. 4. 5.]
 [5. 4. 3. 4. 3. 4. 5. 4.]
 [6. 5. 4. 3. 4. 5. 6. 5.]]
Out[111]:
4.0

Złożoność algorytmu¶

  • złożonść czasowa $O(|x|*|y|)$
  • złożoność pamięciowa $O(|x|*|y|)$

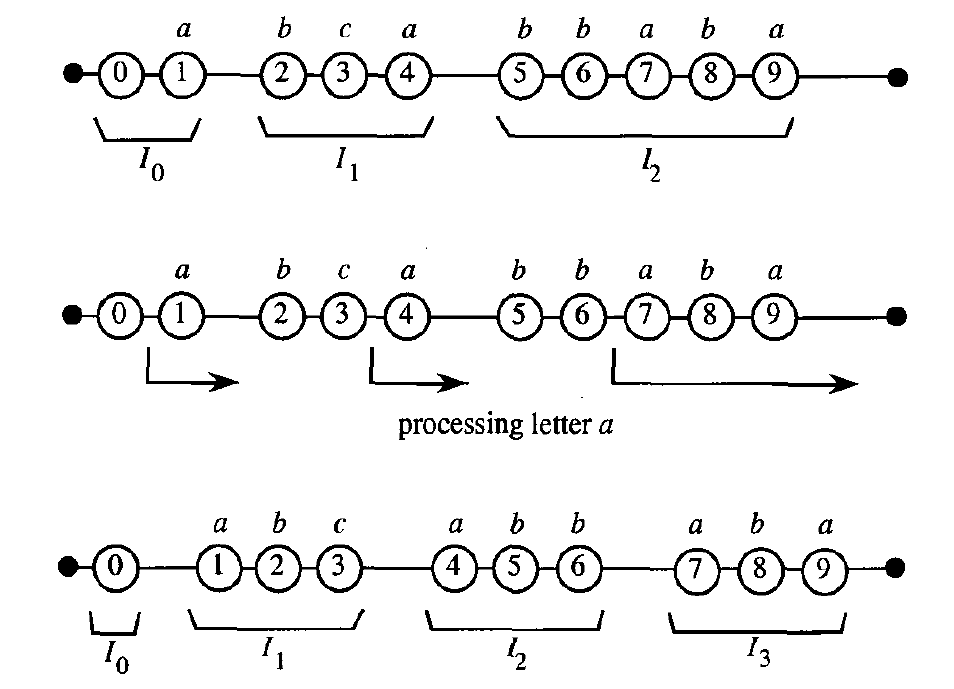
Altrenatywny algorytm obliczania LCS¶

y = cb a

Oznaczenia¶

$I_k = \{j: lcs(x[1..i-1], y[1..j]) = k\}$ - partycja o indeksie $k$

$CLASS(i)$ - numer $k$ partycji $I_k$, do której należy litera o indeksie $i$

$SPLIT(I_k, p) = ([f, f+1, ..., p-1], [p, p+1, ..., g])$ - jeśli $p$ należy do partycji $[f, f+1, f+2, ..., g]$ oraz $p \neq f$

$UNION(I_k, I_{k+1})$ - połączenie dwóch rozłącznych, następujących po sobie partycji

In [2]:
from bisect import bisect

def lcs2(x,y):
    ranges = []
    # ranges[i] zawiera pythonowy indeks pierwszego 
    # elementu dla przedziału i+1 (!)
    ranges.append(len(y)) 
    y_letters = list(y)
    for i in range(len(x)):
        positions = [j for j, l in enumerate(y_letters) if l == x[i]]
        positions.reverse()
        for p in positions:
            k = bisect(ranges, p)
            if(k == bisect(ranges, p-1)):
                if(k < len(ranges) - 1):
                    ranges[k] = p
                else:
                    ranges[k:k] = [p]
    return len(ranges) - 1
In [21]:
lcs3("zcbbda", "abcabbazba")

------------------------------
[10]
0: abcabbazba
-> z
------------------------------
[7, 10]
0: abcabba
1: zba
-> c
------------------------------
[2, 10]
0: ab
1: cabbazba
-> b
------------------------------
[1, 4, 10]
0: a
1: bca
2: bbazba
-> b
------------------------------
[1, 4, 5, 10]
0: a
1: bca
2: b
3: bazba
-> d
------------------------------
[1, 4, 5, 10]
0: a
1: bca
2: b
3: bazba
-> a
------------------------------
[0, 3, 5, 6, 10]
0: 
1: abc
2: ab
3: b
4: azba
Out[21]:
4

Inne algorytmy podobieństwa łańcuchów znaków¶

  • odległość Damerau–Levenshtein - dopuszczamy zamianę kolejności dwóch sąsiednich liter
  • współczynnik Sørensena–Dice'a - $\frac{2|X\cap Y|}{|X| + |Y|}$
  • odległość Hamminga, dla łańcuchów o tej samej długości = liczba pozycji, na których łańcuchy się różnią
  • współczynnik Jaccarda - $\frac{|X\cap Y|}{|X \cup Y|}$

Podobieństwo Jaro-Winklera¶

$sim_w = sim_j + lp(1-sim_j)$

  • $sim_w$ - podobieństwo Winklera
  • $l$ - długość wspólnego prefiksu ($l \leq 4$)
  • $p$ - współczynnik skalujący ($p \leq 0.25$, zwykle $0.1$)

$sim_j = \frac{1}{3}\left( \frac{m}{|s_1|} + \frac{m}{|s_2|} + \frac{m-t}{m} \right), m > 0$

  • $|s_i|$ - długość łańcucha $s$
  • $m$ - liczba pasujących znaków
  • $t$ - liczba transpozycji

Pasujące znaki¶

Znaki pasują do siebie, jeśli są identyczne i nie są oddalone od siebie o więcej niż $\left\lfloor \frac{max(|s_1|, |s_2|)}{2}\right\rfloor-1$